-
[Algorithm] 네트워크 플로우 (Network Flow)Problem Solving/Algorithm 2020. 3. 9. 00:59
네트워크 플로우 (Network Flow) 란?
- 각 노드의 용량이 정해진 상태에서, 시작점에서 끝점까지 흐르는 최대 유량을 구하는 알고리즘
- 네트워크 데이터 전송, 교통 체증, 물류 시스템 등에 활용
[용어]
- S : 시작점 (Source)
- T : 도착점 (Sink)
- c(a, b) : a에서 b로 흐를 수 있는 최대 양 (Capacity)
- f(a, b) : a에서 b로 흐른 실제 양 (Flow)
[제약 조건]
- 용량 제한 속성 : f(u, v) <= c(u, v)
- *유량의 대칭성 : f(u, v) == -f(u, v)
- 나오는 유량의 합 == 들어오는 유량의 합네트워크 플로우 구현 방법
- 포드 풀커슨 알고리즘 (Ford-Fulkerson Algorithm)
- 에드몬드 카프 알고리즘 (Edmonds Karp Algorithm)
[구현 방법]
- S에서 T로 가는 증가 경로 구하기
(단, 경로의 순서는 상관 없으며, 용량이 흐를 수 있는 상태인 경로이면 가능함.)
- 경로의 모든 간선에 f 만큼의 유량 추가
- 더 이상의 증가 경로가 없을 때까지 반복 수행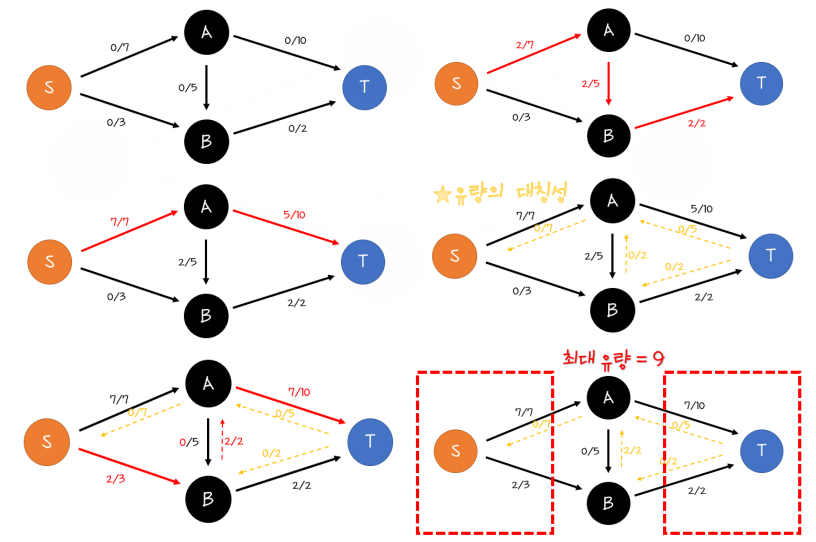
# 포드 풀커슨 알고리즘 (Ford-Fulkerson Algorithm)
- DFS 기반의 알고리즘
- 시간 복잡도 : O($EF$)
시간 복잡도가 F와 관련되어, F값이 클 경우 최악의 상황이 발생할 수 있다.
해당 상황은 BFS를 이용하여 증가 경로를 구하는 기법인 에드몬드 카프 알고리즘을 통해 방지할 수 있다.
[최악의 상황 예시]

해당 상황일 경우 flow가 1씩 흐르는 경로가 반복되어 낭비가 발생할 수 있다.
[Ford-Fulkerson Algorithm Code]
#include <cstdio> #include <queue> #include <vector> #include <cstring> #include <algorithm> #define MAX 100 //가능한 최대 노드 갯수 #define INF 999999999 using namespace std; int c[MAX][MAX], f[MAX][MAX], visit[MAX]; vector<int> adj[MAX]; //인접 노드 배열 int maxFlow(int S, int T); int dfs(int a, int T, int flow); int main() { //printf("%d\n", maxFlow(S, T)); return 0; } int maxFlow(int S, int T) { int result = 0; while (1) { memset(visit, 0, sizeof(visit)); //모든 정점 방문 초기화 int flow = dfs(S, T, INF); if (!flow) break; result += flow; } return result; } int dfs(int a, int T, int flow) { //dfs 모든 경로 탐색 if (visit[a]) return 0; visit[a] = 1; if (a == T) return flow; //도착지에 도달한 경우 최소 flow 값 반환 for (int i = 0; i < adj[a].size(); i++) { int b = adj[a][i], now_flow = c[a][b] - f[a][b]; if (now_flow <= 0) continue; int result = dfs(b, T, min(flow, now_flow)); if (result) { //최소 유량 추가 f[a][b] += result; f[b][a] -= result; return result; } } return 0; }# 에드몬드 카프 알고리즘 (Edmonds-Karp Algorithm)
- BFS 기반의 알고리즘
- 보통 많이 사용되는 알고리즘
- 시간 복잡도 : O($VE^{2}$)
[Edmonds-Karp Algorithm Code]
#include <cstdio> #include <queue> #include <vector> #include <cstring> #include <algorithm> #define MAX 100 //가능한 최대 노드 갯수 #define INF 999999999 using namespace std; int c[MAX][MAX], f[MAX][MAX], visit[MAX]; vector<int> adj[MAX]; //인접 노드 배열 int maxFlow(int S, int T); int bfs(int S, int T); int main() { //printf("%d\n", maxFlow(s, t)); return 0; } int maxFlow(int S, int T) { int result = 0; while (1) { int flow = bfs(S, T); if (!flow) break; result += flow; } return result; } int bfs(int S, int T) { memset(visit, -1, sizeof(visit)); //모든 정점 방문 초기화 queue<int> q; //bfs 모든 경로 탐색 q.push(S); while (!q.empty()) { int a = q.front(); q.pop(); for (int i = 0; i < adj[a].size(); i++) { int b = adj[a][i]; //방문하지 않은 노드 중, 용량이 남아 있는 경우 확인 if (c[a][b] - f[a][b] <= 0) continue; if (visit[b] != -1) continue; q.push(b); visit[b] = a; //경로 기억 (a -> b) if (b == T) break; //도착지 도달한 경우 종료 } } if (visit[T] == -1) return 0; //모든 경로 탐색한 경우 종료 int flow = INF; //경로 중 최소 값 저장해야 하므로 초기값 INF for (int i = T; i != S; i = visit[i]) { //최소 유량 탐색 flow = min(flow, c[visit[i]][i] - f[visit[i]][i]); } for (int i = T; i != S; i = visit[i]) { //최소 유량 추가 f[visit[i]][i] += flow; f[i][visit[i]] -= flow; } return flow; }[관련 문제]
https://www.acmicpc.net/problem/6086
https://www.acmicpc.net/problem/7616
[참고]
http://blog.naver.com/PostView.nhn?blogId=kks227&logNo=220804885235
http://kocw.xcache.kinxcdn.com/KOCW/document/2019/pusan/chohwangue0102/7.pdf
'Problem Solving > Algorithm' 카테고리의 다른 글
[Algorithm] 최소 신장 트리 (MST, Minimum Spanning Tree) (2) 2020.03.08 댓글